1. TensorFlow模块与架构介绍
TensorFlow模块与APIs
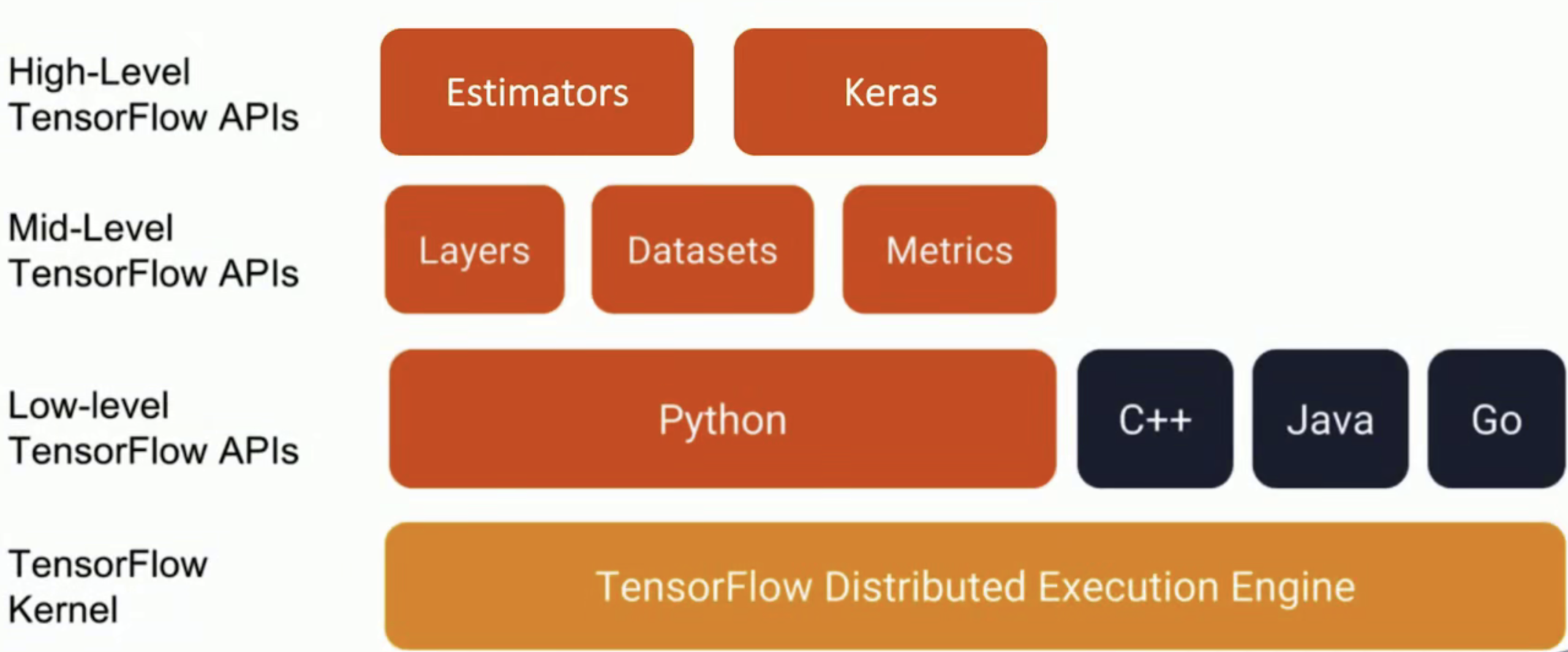
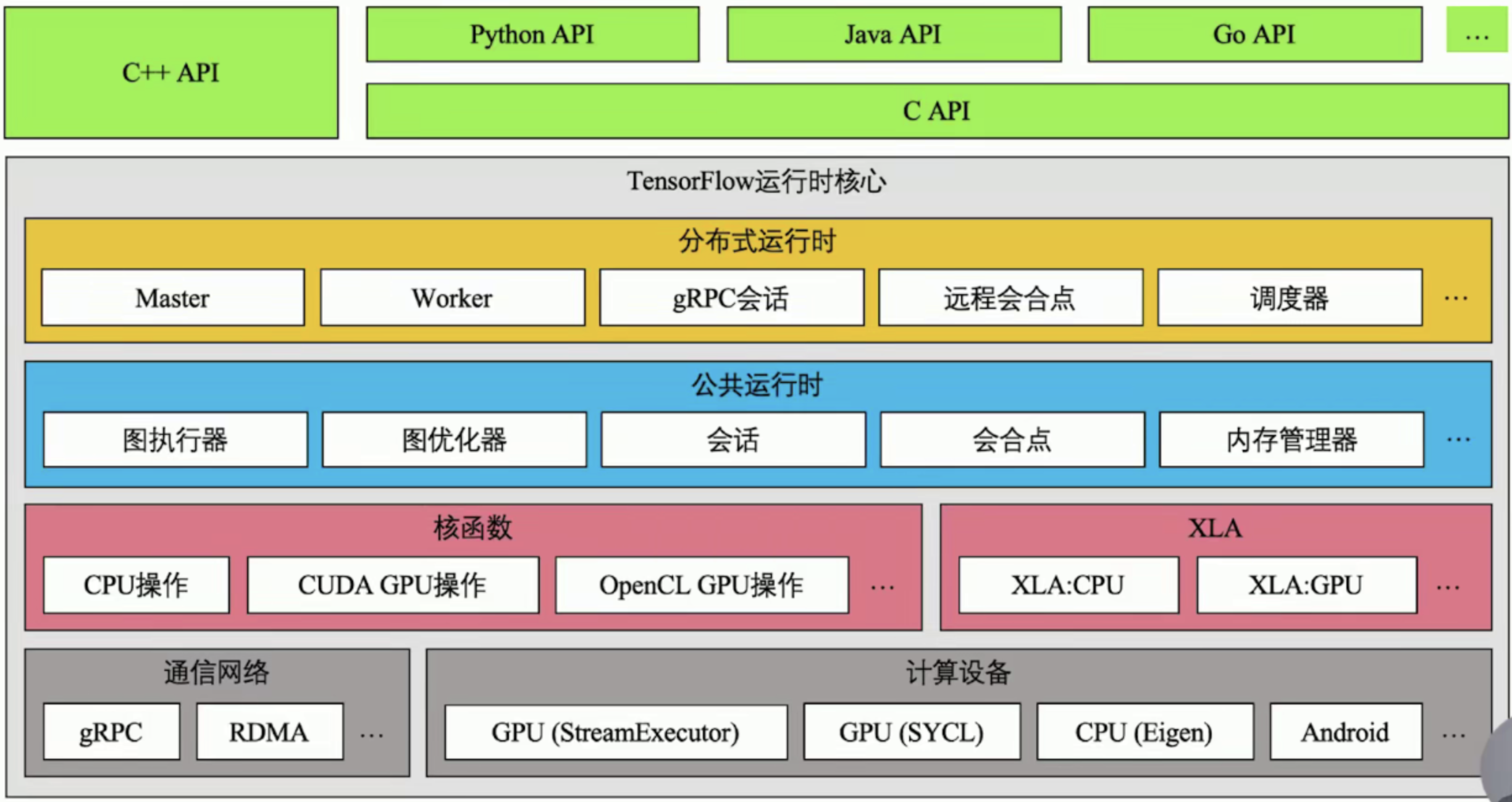
TensorFlow架构
2. TensorFlow数据流图介绍
声明式编程与命令式编程的多角度对比
| 编程范式 | 核心思想 | 程序抽象 | 计算过程 | 计算单元 | 擅长领域 | 实现方式 |
|---|---|---|---|---|---|---|
| 声明式编程 | 要什么 | 数学模型 | 表达式变换 | 函数 | 数理逻辑 | 结构化、抽象化 |
| 命令式编程 | 怎么做 | 有穷自动机 | 状态转换 | 指令 | 业务逻辑 | 过程化、具体化 |
斐波拉契数列示例
声明式编程
fib = lambda x : 1 if x <= 2 else fib(x - 1) + fib(x - 2)
命令式编程
def fib(n):
a, b = 1, 1
for i in range(1, n):
a, b = b, a + b;
return a;
TensorFlow数据流图是一种声明式编程范式
TensorFlow数据流图
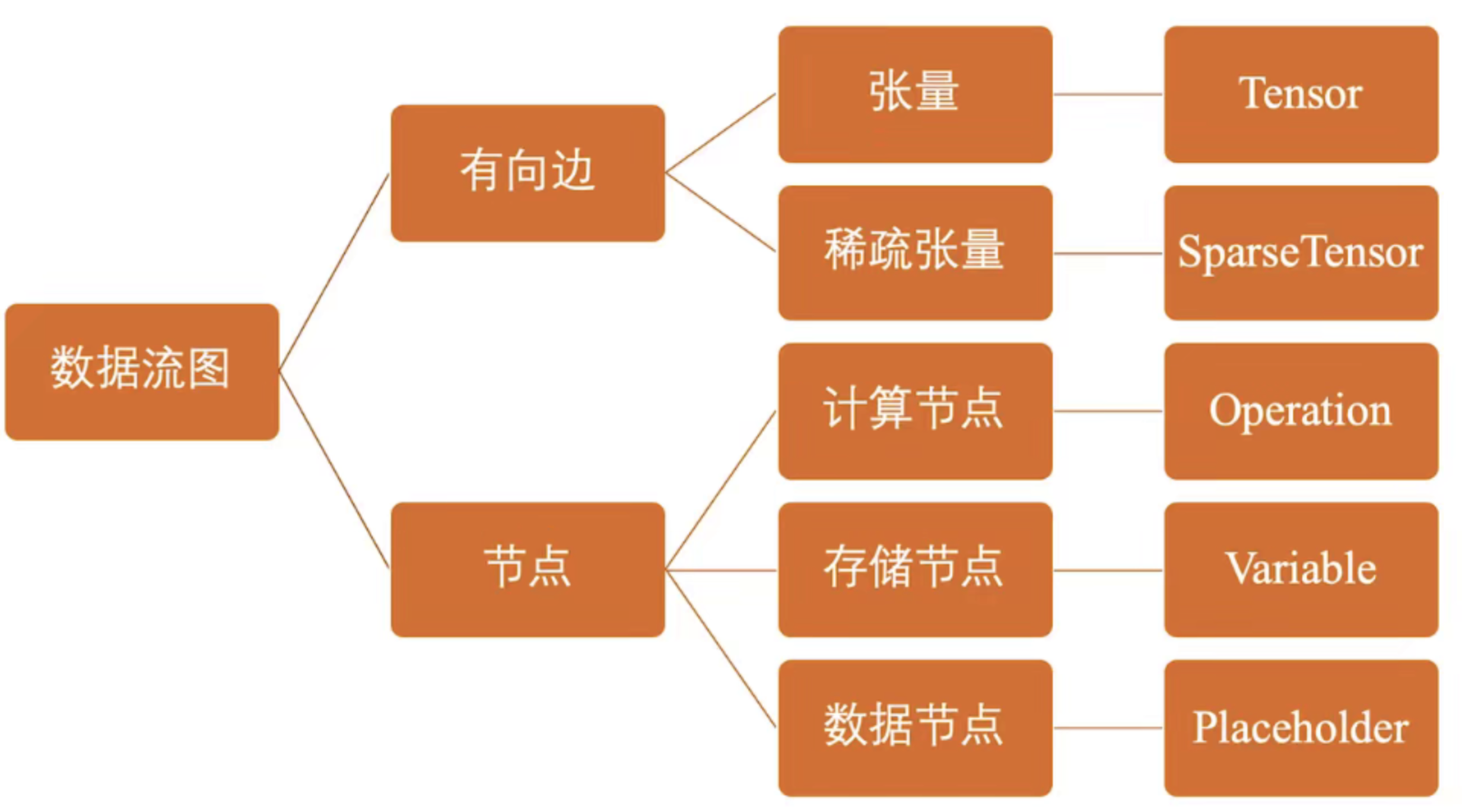
张量在TensorFlow中可以简单理解为数据
Variable存储模型迭代更新的参数
TensorFlow数据流图优势
- 并行计算快
- 分布式计算快(CPUs、GPUs、TPUs)
- 预编译优化(XLA)
- 可移植性好(Language-independent representation)
3. 张量(Tensor)是什么
在数学里,张量是一种几何实体,广义上表示任意形式的“数据”,张量可以理解为0阶标量、1阶向量和2阶矩阵在高维空间上的推广,张量的阶描述它表示数据的最大维度。
| 阶 | 数据实体 | Python样例 |
|---|---|---|
| 0 | 标量 | scalar = 1 |
| 1 | 向量 | vector = [1,2,3] |
| 2 | 矩阵(数据表) | matrix = [[1,2,3],[4,5,6],[7,8,9]] |
| 3 | 数据立方 | tensor = [[[1],[2],[3]],[[4],[5],[6]],[[7],[8],[9]], ...] |
| n | n阶张量 | ... |
在TensorFlow中,张量(Tensor)表示某种相同数据类型的多维数组。
因此,张量有两个重要属性:
- 数据类型(如浮点型、整型、字符串)
- 数组形状(各维度的大小)
TensorFlow张量是什么?
- 张量是用来表示多维数据的
- 张量是执行操作时的输入或输出数据
- 用户通过执行操作来创建或计算张量
- 张量的形状不一定在编译时确定,可以在运行时通过形状推断计算得出
在TensorFlow中,有几类比较特别的张量,由以下操作产生
- tf.constant // 常量
- tf.placeholder //占位符
- tf.Variable // 变量
4. 变量(Variable)是什么
变量是一种特殊的张量,主要作用是维护特定结点的状态,如深度学习或机器学习的模型参数。
tf.Variable 方法是操作,返回值是变量(特殊张量)。
通过tf.Variable方法创建的变量,与张量一样,可以作为操作的输入和输出。不同之处在于:
- 张量的生命周期通常随依赖的计算完成而结束,内存也随即释放。
- 变量则常驻内存,在每一步训练时不断更新其值,以实现模型参数的更新。
# 创建变量
w = tf.Variable(<initial-value>, name=<optional-value>)
# 将变量作为操作的输入
y = tf.matmul(w, ...anothor variable or tensor)
z = tf.sigmoid(w + y)
# 使用assign或assign_xxx方法重新给变量赋值
w.assign(w + 1.0)
w.assign_add(1.0)
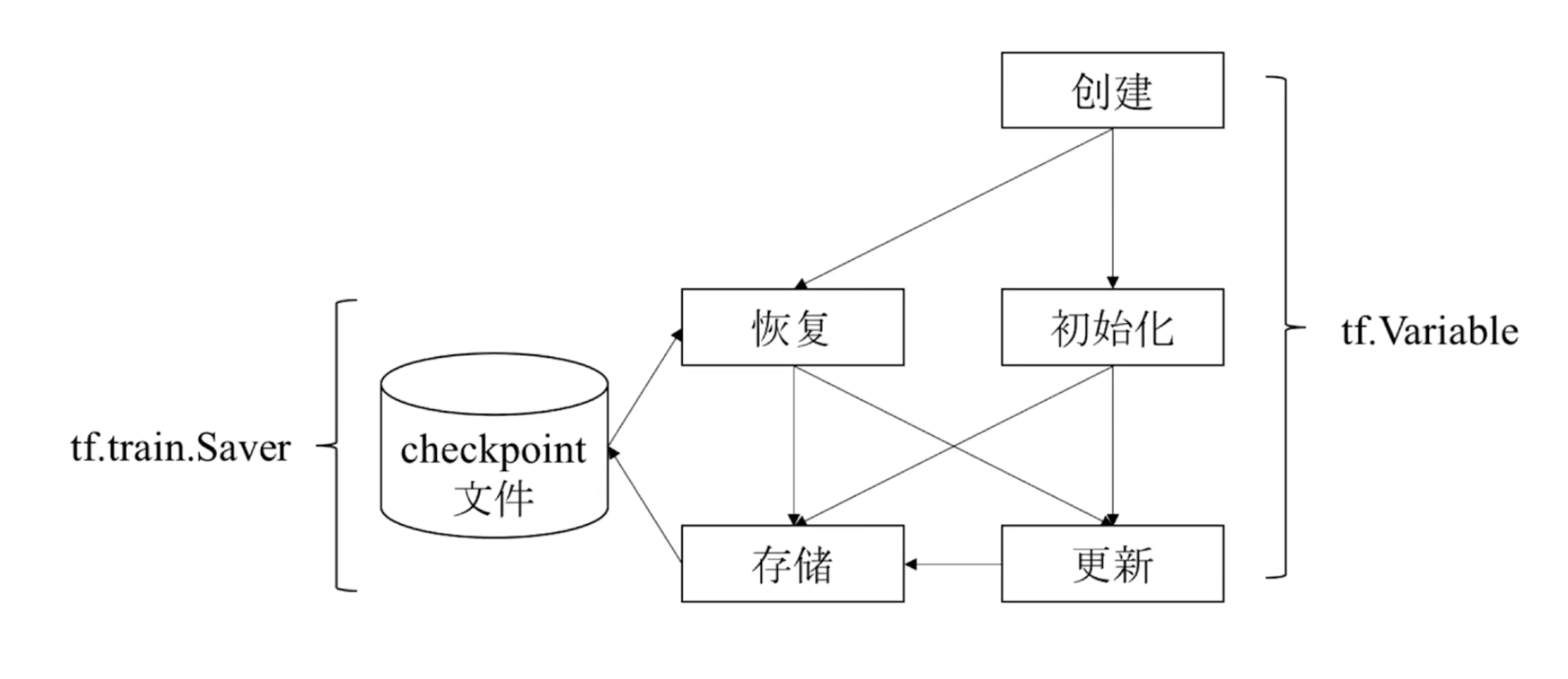
Tensorflow变量使用流程
5. 操作(Operation)是什么
TensorFlow用数据流图表示算法模型。数据流图由节点和有向边组成,每个节点匀对应一个具体的操作。因此,操作是模型功能的实际载体。
数据流图中的节点按照功能不同可以分为三种:
- 存储节点:有状态的变量操作,通常用来存储模型参数;
- 计算节点:无状态的计算或控制操作,主要负责算法逻辑表达或流程控制;
- 数据节点:数据的占位符操作,用于描述,图外输入数据的属性。
操作的输入或输出是张量或操作(函数式编程)
TensorFlow典型计算和控制操作
| 操作类型 | 典型操作 |
|---|---|
| 基础算术 | add/multiply/mod/sqrt/sin/trace/fft/argmin |
| 数组运算 | size/rank/split/reverse/cast/one_hot/quantize |
| 梯度裁剪 | clip_by_value/clip_by_norm/clip_by_global_norm |
| 逻辑控制和调试 | identity/logic_and/equal/less/is_finite/is_nan |
| 数据流控制 | enqueue/size/take_grad/apply_grad |
| 初始化操作 | zero_initialzer/random_normal_initianlizer/orthogonal_initializer |
| 神经网络运算 | convolution/pool/bias_add/softmax/dropout/erosion2d |
| 随机运算 | random_normal/random_shuffle/multinomial/random_gamma |
| 字符串函数 | string_to_hash_bucket/reduce_join/substr/encode_base64 |
| 图像处理运算 | encode_png/resize_images/rot90/hsv_to_rgb/adjust_gamma |
TensorFlow占位符
TensorFlow使用占位符操作表示图外输出的数据,如训练和测试数据。
TensorFlow数据流图描述了算法模型的计算拓扑,其中各个操作(节点)都是抽象的函数映射或数学表达式。
换句话说,数据流图本身是一个具有计算拓扑和内部结构的“壳”。在用户向数据流图填充数据前,图中并没有真正执行任何计算。
TensorFlow Python API 和 Python 本身的API要区分出来,Python只是一种语言,TensorFlow Python API是领域特定语言。
6. 会话(Session)是什么
会话提供了估算张量和执行操作的运行环境,它是发放计算的客户端,所有计算任务都由它连接的执行引擎完成。一个会话的典型使用流程分为以下3步。
# 1. 创建会话
session = tf.Session(target=..., graph=..., config=...)
# 2. 估算张量或执行操作
session.run(...)
# 3. 关闭会话
session.close()
Session参数
|参数名称|说明|
|-------|-------|
|target|会话连接的执行引擎|
|graph|会话加载的数据流图|
|config|会话启动时的配置项|
获取张量值的另外两种方法:估算张量(Tensor.eval)与执行操作(Operation.run)
tf.global_variables_initializer().run()
fetch = y.eval(feed_dict={x: 3.0})
TensorFlow会话执行
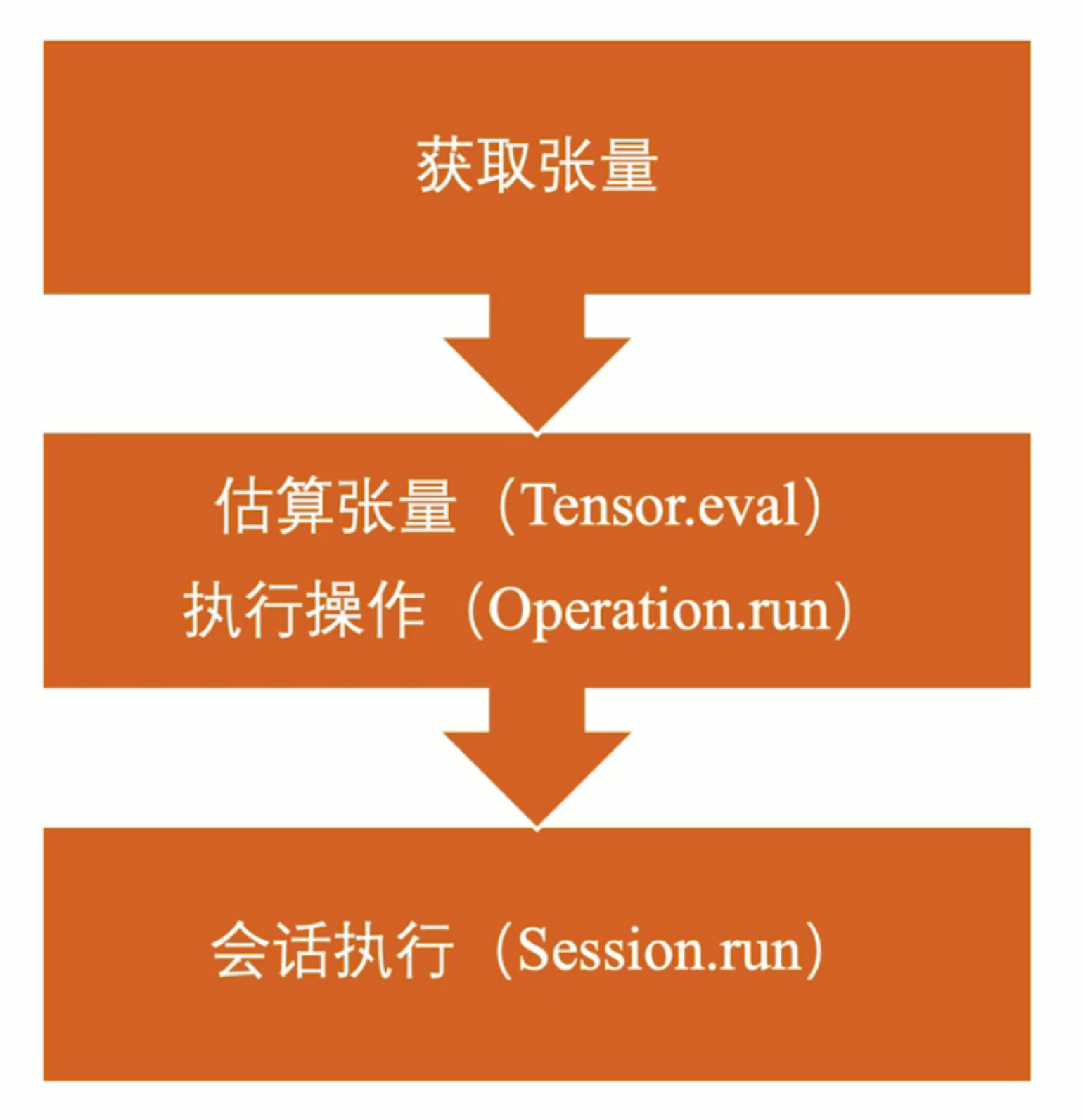
TensorFlow会话执行原理
当我们调用session.run(train_op)语句执行训练操作时:
- 首先,程序内部提取操作依赖的所有前置操作,这些操作的节点共同组成一副子图。
- 然后,程序会将子图中的计算节点、存储节点和数据节点按照各自的执行设备分类,相同设备上的节点组成了一幅局部图。
- 最后,每个设备上的局部图在实际执行时,根据节点间的依赖关系将各个节点有序地加载到设备上执行。
TensorFlow会话本地执行
对于单机程序来说,相同机器上不同编号的CPU或GPU就是不同的设备,我们可以在创建节点时指定该节点的设备。
# 在0号CPU执行的存储节点
with tf.device("/cpu:0")
v = tf.Variable(...)
# 在0号GPU执行的计算节点
with tf.device("/gpu:0")
v = tf.matmul(...)
7. 优化器(Optimizer)是什么
前置知识:损失函数
损失函数是评估特定模型参数和特定输入时,表达模型输出的推理值与真实值之间不一致程度的函数。
常见的损失函数有平方损失函数、交叉熵损失函数和指数损失函数。
使用损失函数对所有训练样本求损失值,再累加求平均可得到模型的经验风险。
然而,如果过度地追求训练数据上的低损失值,就会遇到过拟合问题。训练集通常并不能完全代表真实场景的数据分布。当两者的分布不一致时,如果过分依赖训练集上的数据,面对新数据时就会无所适从,这时模型的泛化能力就会变差。
模型训练的目标是不断最小化经验风险。随着训练步数的增加,经验风险将逐渐降低,模型复杂度也将逐渐上升。为了降低过度训练可能造成的过拟合风险,可以引入专门用来度量模型复杂度的正则化项(regularizer)或惩罚项(penalty term)。常用的正则化项为L0、L1和L2范数。因此,我们将模型最优化的目标替换为鲁棒性更好的结构风险最小化(structual risk minimization, SRM)。由经验风险和正则项两部分构成。
在模型训练过程中,结构风险不断地降低。当小于我们设置的损失阈值时,则认为此时的模型已经满足需求。因此,模型训练的本质就是在最小化结构风险的同时取得最优的模型参数。
前置知识:优化算法
典型的机器学习和深度学习问题通常都需要转换为最优化问题进行求解。
求解最优化问题的算法称为优化算法,它们通常采用迭代方式实现:首先设定一个初始的可行解,然后基于特定的函数反复重新计算可行解,直到找到一个最优解或达到预设的收敛条件。不同的优化算法采用的迭代策略各有不同:
- 有的使用目标函数的一阶导数,如梯度下降法;
- 有的使用目标函数的二阶导数,如牛顿法;
- 有的使用前几轮迭代的信息,如Adam。
基于梯度下降法的迭代策略最简单,它直接沿着梯度负方向,即目标函数减少最快的方向进行直线搜索。
TensorFlow训练机制
典型的机器学习和深度学习问题,包含收下3个部分:
- 模型: y=f(x)=wx+b,其中x是输入数据,y是模型输出的推理值,w和b是模型参数,即用户的训练对象。
- 损失函数:
- 优化算法:
TensorFlow优化器
优化器实现优化算法的载体。
一次典型的迭代优化应该为分以下3个步骤:
- 计算梯度:调用compute_gradients方法;
- 处理梯度:用户按照自己需求处理梯度值,如梯度裁剪和梯度加权等;
- 应用梯度:调用apply_gradients方法,将处理后的梯度值应用到模型参数。
# 1. 计算梯度
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.01)
grads_and_vars = optimizer.compute_gradients(loss, var_list, ...)
# 2. 处理梯度
clip_grads_and_vars = [(tf.clip_by_value(grad, -1.0, 1.0), var]
for grad, var in grads_and_vars]
# 3. 应用梯度
train_op = optimizer.apply_gradients(clip_grads_and_vars)